Page 65 - 网络电信2024年2月刊
P. 65
式中,w 0 为光束的束腰半径,本文选取w 0 =0.075rad。
光子的初始方向矢量为[24]:
(23) (26)
D.光子的单次散射率
光子在复合信道中经过碰撞后,一部分能量被吸收,另一
B.计算光子步长 部分能量散射后继续传输。为了量化碰撞后光子的能量,定义
光子在两次散射之间的步长通过累计概率分布计算。由 ω 0 为介质的单次散射率,即散射部分的能量与总衰减能量的比
于光子在水体中运动时会受到水体及水体中各种成分的衰减作 值,如下式所示:
用,因此光子在海洋信道中两次散射之间的实际步长为[24]:
(27)
(24)
根据式(27),在表4中给出了三种海水水质下不同密度气泡
式中,ε 2 为(0,1)之间的随机数;c(λ)为包含气泡群散射 群的复合信道的单次散射率。
的复合信道的衰减系数。
表4 三种海水水质下不同密度气泡群的 复合信道的单次散射率
C.确定光子运动方向
光子发生碰撞后的方向由散射角θ和方位角 决定,其方
向矢量如式(25)[24]所示:
(25)
方位角 为[0,2π]范围内的随机值,散射角θ由散射相函
数抽样获得。由于复合信道的散射相函数形式复杂,无法用数 四、仿真结果与分析
学公式表达,不能直接用于对散射角抽样,因此本文使用拒绝 4.1 接收端光斑弥散情况及空间能量分布
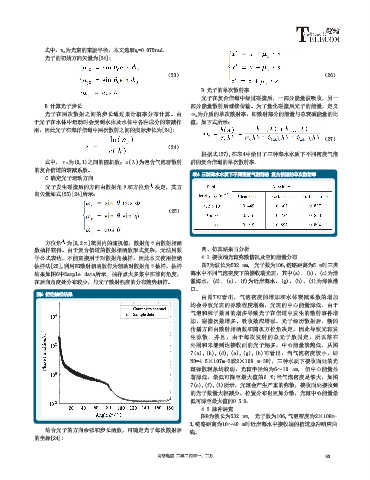
抽样法[25],利用HG散射相函数作为辅助对散射角θ抽样,抽样 图7为波长为532 nm, 光子数为106,链路距离为5 m时三类
结果如图6中Sample data所示。抽样点大多集中在前向角度, 海水中不同气泡密度下的接收端光斑,其中(a)、(b)、(c)为清
在后向角度处分布较少,与光子散射强度的分布趋势相符。 澈海水,(d)、(e)、(f)为近岸海水,(g)、(h)、(i)为浑浊港
口。
图6 拒绝抽样结果
由图7可看出,气泡密度的增加和水体衰减系数的增加
均会导致光斑的弥散程度增强,光斑的中心能量降低。由于
气泡和粒子数目的增多导致光子在信道中发生的散射事件增
加、碰撞次数增多、吸收效应增强。光子经历散射后,新的
传播方向由散射相函数和随机方位角决定,因此导致光斑发
生弥散。并且,由于每次发射的总光子数固定,所以落在
外围和未能到达接收面的光子越多,中心能量就越低。从图
7(a),(b),(d),(e),(g),(h)可看出,当气泡密度较小,即
N0=4.5×107m-3或2×108 m-3时,三种水质下接收面处的光
斑弥散现象均较弱,光斑半径约为6~10 cm, 但中心能量显
著降低,最低可降至最大值的6 %;当气泡密度足够大,如图
7(c),(f),(i)所示,光斑会产生严重的弥散,接收面处接收到
的光子数量大幅减少,位置分布也更加分散,光斑中心能量最
低可降至最大值的0.5 %。
4.2 脉冲展宽
图8为波长为532 nm, 光子数为106,气泡密度为2×108m-
3,链路距离为10~40 m时近岸海水中接收端的信道脉冲响应曲
结合光子的方向余弦和步长函数,可确定光子每次散射后
线。
的坐标[24]:
网络电信 二零二四年一、二月 63