Page 64 - 网络电信2024年2月刊

3.1 复合信道光学特性参数分析 下[16]:
3.1.1 复合信道的吸收与散射
根据海水的固有光学特性(IOPs)模型[22],复合信道的吸收 （20）
系数a(λ)可建模为各成分吸收系数之和，如下式： 式中，g为非对称因子，即散射角余弦的平均值 ,不同
a(λ)=a W (λ)+a phy (λ)+a NAP (λ)+a CDOM (λ) (15) 环境海水g的取值不同。g越接近-1,后向散射概率高于前向散
式中，λ为光波长，a W (λ),a phy (λ),a NAP (λ)和a CDOM (λ)分 射；g越接近于0,介质的散射越接近各向同性；而g越接近1,介
别为纯水、浮游植物、非藻类颗粒以及有色溶解有机物的吸收 质的前向散射越强，仿真时g取0.924。
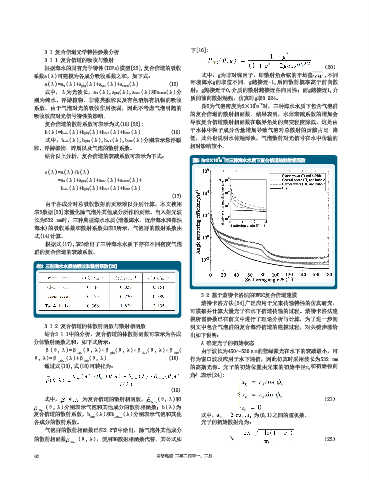
8 -3
系数。由于气泡对光的吸收作用极弱，因此不考虑气泡引起的 图5为气泡密度为2×10 m 时，三种海水水质下包含气泡群
吸收效应对光信号特性的影响。 的复合信道的散射相函数。结果表明，水体衰减系数的增加会
复合信道的散射系数可表示为式(16)[22]: 导致复合信道散射相函数在临界角处的突变程度降低，这是由
b(λ)=b sus (λ)+b phy (λ)+b det (λ)+b bub (λ) (16) 于水体中粒子成分含量增加导致气泡对总散射的贡献占比 降
式中，b sus (λ),b phy (λ),b det (λ),b bub (λ)分别表示悬浮颗 低，此外也说明水体越浑浊，气泡散射对光信号在水中传输的
粒、浮游植物、碎屑以及气泡的散射系数。 相对影响较小。
结合以上分析，复合信道的衰减系数可表示为下式：
8 -3
图5 N 0 =2×10 m 时三种海水水质下复合信道的散射相函数
c(λ)=a(λ)+b(λ)
=a W (λ)+a phy (λ)+a NAP (λ)+a CDOM (λ)+
b sus (λ)+b phy (λ)+b det (λ)+b bub (λ)
(17)
由于各成分对总吸收散射的贡献难以分别计算，本文使用
表2数据[23]来量化除气泡外其他成分所作的贡献。当入射光波
长为532 nm时，三种典型海水水质(清澈海水、近岸海水和浑浊
海水)的吸收系数和散射系数如表2所示，气泡群的散射系数由
式(14)计算。
根据式(17),表3给出了三种海水水质下存在不同密度气泡
群的复合信道的衰减系数。

表2 三种海水水质的吸收和散射系数[23]

3.2 基于蒙特卡洛法的UWOC复合信道建模
蒙特卡洛方法[24]广泛应用于光束传输特性的仿真研究，
可模拟并计算大量光子在水下信道传输的过程。蒙特卡洛法建
模所需参数已在前文中进行了理论分析与计算，为了进一步阐
3.1.2 复合信道的体散射函数与散射相函数 明文中包含气泡群的复合海洋信道的建模过程，对关键步骤给
结合3.1.1中的分析，复合信道的体散射函数可表示为各成 出如下说明：
分体散射函数之和，如下式所示： A.确定光子的初始状态
β(θ,λ)=β sus (θ,λ)+β phy (θ,λ)+β det (θ,λ)+β bub ( 由于波长为450～530μm的蓝绿激光在水下的衰减最小，可
θ,λ)=β other (λ)+β bub (θ,λ) (18) 作为窗口波段应用于水下通信，因此仿真时采用波长为532 nm
通过式(13),式(18)可转化为： 的高斯光源。光子的初始位置由光束的初始半径r 0 和初始径向
角 表示[24]:

(19)
式中， 为复合信道的散射相函数， (θ,λ)和 （21）
(θ,λ)分别表示气泡和其他成分的散射相函数；b(λ)为
复合信道的散射系数，b bub (λ)和b other (λ)分别表示气泡和其他 式中， 为(0,1)之间的随机数。
各成分的散射系数。 光子的初始散射角为：
气泡群的散射相函数已在2.2节中给出，除气泡外其他成分
的散射相函数 (θ,λ)，使用HG散射相函数代替。其公式如 （22）

62 网络电信 二零二四年一、二月