Page 63 - 网络电信2024年2月刊

光 通 信

Wu等人定义了一个更广义的Junge谱分布，其表达式为 其中，b bub (λ)为气泡群的散射系数，计算如下[22]:
[21]:
（14）
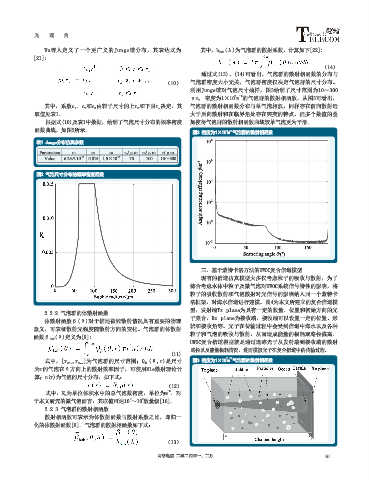
通过式(13)、(14)可看出，气泡群的散射相函数的分布与
（10） 气泡群密度大小无关，气泡群密度仅决定气泡群的尺寸分布。
利用Junge谱对气泡尺寸抽样，图3绘制了尺寸范围为10～300
7 -3
μm, 密度为1×10 m 的气泡群的散射相函数。从图3可看出，
其中，系数c 1 、c 2 和c 3 由粒子尺寸的上r b 和下限r a 决定，其 气泡群的散射相函数分布与单气泡相似，同样存在前向散射远
取值见表1。 大于后向散射和在临界角处存在突变的特点，但多个数值的叠
根据式(10)及表1中数据，绘制了气泡尺寸分布的概率密度 加使得气泡群的散射相函数曲线较单气泡更为平滑。
函数曲线，如图2所示。 7 -3
图3 密度为1×10 m 气泡群的散射相函数
表1 Junge分布仿真参数
Parameters c 1 c 2 c 3 r a /μm r b /μm r/μm
Value 6.25×10 -10 0.015 1.5×10 -10 70 100 10～300

图2 气泡尺寸分布的概率密度函数

三、基于蒙特卡洛方法的UWOC复合信道模型
现有的信道仿真模型大多仅考虑粒子的吸收与散射，为了
综合考虑水体中粒子及微气泡对UWOC系统信号特性的影响，将
粒子的吸收散射和气泡散射对光信号的影响纳入同一个蒙特卡
洛框架，对海水信道进行建模。图4为本文所建立的复合信道模
型，发射端Tx plane为具有一定的数量、位置和初始方向的光
2.2.2 气泡群的体散射函数
子集合，Rx plane为接收端，接收端可以设置一定的位置、形
体散射函数β(θ)对于描述微粒散射情况具有重要的物理
状和接收角等。光子在传输过程中会受到信道中海水以及各种
意义，可表征散射光强度随散射方向的变化。气泡群的体散射
粒子和气泡的吸收与散射，从而造成能量的损耗或路径偏离。
函数β bub (θ)定义为[8]:
UWOC复合信道模型就是通过追踪光子从发射端到接收端的散射
路径以及能量损耗情况，进而模拟光子在复合信道中的传输过程。
(11)
7 -3
式中，[r min ,r max ]为气泡群的尺寸范围；Q β (θ,r)是尺寸 图3 密度为1×10 m 气泡群的散射相函数
为r的气泡在θ方向上的散射效率因子，可使用Mie散射理论计
算；n(r)为气泡的尺寸分布，如下式：
（12）
-3
式中，N 0 为单位体积水中的总气泡数密度，单位为m 。对
8
6
于本文研究的微气泡而言，其取值可达10 ～10 数量级[16]。
2.2.3 气泡群的散射相函数
散射相函数可表示为体散射函数与散射系数之比，即归一
化的体散射函数[8]。气泡群的散射相函数如下式：

（13）

网络电信 二零二四年一、二月 61