Page 62 - 网络电信2024年2月刊
P. 62
二、海水信道微气泡的光散射特性研究 结合Mie散射系数a n 和b n 以及散射效率因子Q sca ,可得单气泡
2.1 海水单气泡的光散射特性研究 的散射光强度函数F(θ)和散射相函数P(θ)。F(θ)用于描述不
本文的研究对象为半径10~150 μm之间的微气泡,此类气 同方向散射光强度的大小,P(θ)为归一化的散射光强度函数。
泡不易变形且可以在水中存活较长时间[17]。由于此类气泡的 其计算公式如下[20]:
尺寸远大于入射光波长,因此Mie理论是计算其光散射特性的有 (7)
效方法。根据Mie散射理论[18,19],当波长为λ,初始光强为I0
的自然光平行照射至单个气泡时,在散射角为θ且距离散射体R (8)
处的散射光强I s 可表示为式(1)[19]: 根据式(8),相对折射率m=0.75,波长λ=532 nm时不同尺寸
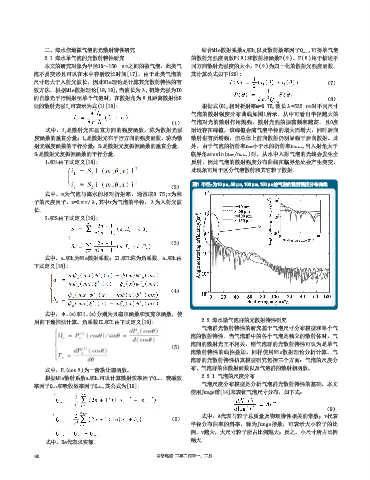
气泡的散射强度分布曲线如图1所示。从中可看出半径越大的
(1) 气泡对光的散射作用越强,散射光强的振荡频率越高。且0度
式中,i 1 是散射光在垂直方向的强度函数,称为散射光强 附近存在峰值,该峰值会随气泡半径的增大而增大,同时后向
度函数的垂直分量;i 2 是散射光在平行方向的强度函数,称为散 散射也有所增强,但总体上前向散射仍明显强于后向散射。此
射光强度函数的平行分量;S 1 是散射光复振幅函数的垂直分量, 外,由于气泡的折射率n bub 小于水的折射率n water ,当入射角大于
S 2 是散射光复振幅函数的平行分量。 临界角arcsin(n bub /n water )时,从水中入射气泡的光线会发生全
i 1 和i 2 由下式定义[18]: 反射,因此气泡的散射强度分布曲线在临界角处会产生突变,
此现象可用于区分气泡散射和其它粒子散射。
图1 半径r为10μm,50μm,100μm,150μm的气泡的散射强度分布曲线
(2)
式中,m为气泡与海水的相对折射率,通常取0.75;x为粒
子的尺度因子,x=2πr/λ,其中r为气泡的半径,λ为入射光波
长。
S 1 和S 2 由下式定义[19]:
(3)
式中,a n 和b n 为Mie散射系数;Π n 和T n 称为角系数。a n 和b n 由
下式定义[18]:
(4)
式中,ψ n (z)和ξ n (z)分别为贝塞尔函数和汉克尔函数,使
用向下递推法计算。角系数Π n 和T n 由下式定义[19]: 2.2 海水微气泡群的光散射特性研究
气泡群光散射特性的研究基于气泡尺寸分布模型和单个气
泡的散射特性。当气泡群中的各个气泡是独立的散射体时,气
泡间的散射光互不相关,则气泡群的光散射特性可认为是单气
(5)
泡散射特性的线性叠加,同样使用Mie散射理论分析计算。气
泡群的光散射特性仿真模型研究包括三个方面:气泡的尺度分
式中,P n (cosθ)为一阶勒让德函数。 布、气泡群的体散射函数以及气泡群的散射相函数。
根据Mie散射系数a n 和b n 可以计算散射效率因子Q sca 、衰减效 2.2.1 气泡的尺度分布
率因子Q ext 和吸收效率因子Q abs ,其公式为[19]: 气泡尺度分布模型是分析气泡群光散射特性的基础,本文
使用Junge谱[14]来表征气泡尺寸分布,如下式:
(9)
式中,A代表与粒子总质量及物理特性相关的常数;v代表
(6)
半径分布曲率的斜率,称为Junge指数,可表示大小粒子的比
例。v越大,大尺寸粒子所占比例越大;反之,小尺寸所占比例
式中,Re代表求实部。 越大。
60 网络电信 二零二四年一、二月